Vierzigeck

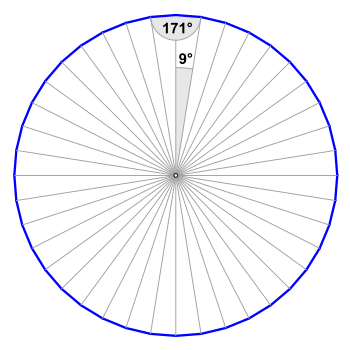
Ein Vierzigeck oder Tetrakontagon ist eine geometrische Figur und ein Vieleck (Polygon). Es ist bestimmt durch vierzig Punkte und deren vierzig Verbindungen namens Strecken, Seiten oder Kanten.

Vierzigecke können eingeteilt werden in:

• überschlagenes Vierzigeck
• nicht überschlagenes Vierzigeck
• konkaves Vierzigeck; mindestens ein Innenwinkel ist größer als 180°
• konvexes Vierzigeck; alle Innenwinkel sind kleiner als 180°
• gleichseitiges Vierzigeck; alle Seiten sind gleich lang
• nach der Anzahl an Symmetrieachsen; es können maximal 40 sein
• Sehnen-Vierzigeck; alle Ecken liegen auf einem gemeinsamen Umkreis
• regelmäßiges Vierzigeck; alle Seiten sind gleich lang, alle Innenwinkel sind gleich groß und alle Eckpunkte liegen auf einem gemeinsamen Umkreis

Im Folgenden wird das regelmäßige Vierzigeck und das regelmäßige überschlagene Vierzigeck betrachtet.

Das regelmäßige Vierzigeck ist nach Carl Friedrich Gauß und Pierre-Laurent Wantzel ein konstruierbares Polygon, da die Anzahl seiner Seiten als Produkt einer Zweierpotenz mit paarweise voneinander verschiedenen Fermatschen Primzahlen (${\displaystyle 40=2^{3}\cdot 5}$) darstellbar ist.

Größen eines regelmäßigen Vierzigecks
Innenwinkel	${\displaystyle {\begin{aligned}\alpha &={\frac {n-2}{n}}\cdot 180^{\circ }={\frac {38}{40}}\cdot 180^{\circ }\\\alpha &=171^{\circ }\end{aligned}}}$
Zentriwinkel (Mittelpunktswinkel)	${\displaystyle {\begin{aligned}\mu &={\frac {360^{\circ }}{40}}\\\mu &=9^{\circ }\end{aligned}}}$
Seitenlänge	${\displaystyle {\begin{aligned}a&=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{40}}\right)\\a&\approx 0{,}156918\cdot R\end{aligned}}}$
Umkreisradius	${\displaystyle {\begin{aligned}R&={\frac {a}{2\cdot \sin \left({\frac {180^{\circ }}{40}}\right)}}\\R&\approx {\frac {a}{0{,}156918}}\end{aligned}}}$
Inkreisradius	${\displaystyle {\begin{aligned}r&=R\cdot \cos \left({\frac {180^{\circ }}{40}}\right)\\r&\approx 0{,}996917\cdot R\end{aligned}}}$
Höhe	${\displaystyle {\begin{aligned}h&=2\cdot r\\h&\approx 1{,}993834\cdot R\end{aligned}}}$
Flächeninhalt	${\displaystyle {\begin{aligned}A&=R^{2}\cdot {\frac {5}{2}}\left({\sqrt {2}}\cdot \left({\sqrt {5}}+1\right)-2\cdot {\sqrt {5-{\sqrt {5}}}}\right)\\A&\approx 3{,}1286893\cdot R^{2}\end{aligned}}}$

Der Innenwinkel ${\displaystyle \alpha }$ wird von zwei benachbarten Seitenkanten eingeschlossen. In der allgemeinen Formel für regelmäßige Polygone steht die Variable ${\displaystyle n}$ für die Anzahl der Eckpunkte des Polygons. In diesem Fall ist für die Variable die Zahl ${\displaystyle 40}$ einzusetzen.

${\displaystyle \alpha ={\frac {n-2}{n}}\cdot 180^{\circ }={\frac {40-2}{40}}\cdot 180^{\circ }={\frac {38}{40}}\cdot 180^{\circ }=171^{\circ }}$

Die Summe der Innenwinkel beträgt ${\displaystyle {(n-2)\cdot 180^{\circ }}=38\cdot 180^{\circ }=6840^{\circ }}$.

Der Zentriwinkel oder Mittelpunktswinkel ${\displaystyle \mu }$ wird von zwei benachbarten Umkreisradien ${\displaystyle R}$ eingeschlossen. In der allgemeinen Formel ist für die Variable ${\displaystyle n}$ die Zahl ${\displaystyle 40}$ einzusetzen.

${\displaystyle \mu ={\frac {360^{\circ }}{n}}={\frac {360^{\circ }}{40}}=9^{\circ }}$

Das Vierzigeck ist in vierzig gleichschenklige Dreiecke sogenannte Teildreiecke teilbar. Aus der Hälfte eines solchen Teildreiecks, sprich aus einem rechtwinkligen Dreieck mit der Kathete (halbe Seitenlänge) ${\displaystyle {\frac {a}{2}}}$, der Hypotenuse (Umkreisradius) ${\displaystyle R}$ und dem halben Zentriwinkel ${\displaystyle {\frac {\mu }{2}}}$ erhält man mithilfe der Trigonometrie im rechtwinkligen Dreieck die Seitenlänge ${\displaystyle a}$ wie folgt

${\displaystyle {\begin{aligned}a&=R\cdot 2\cdot \sin \left({\frac {\mu }{2}}\right)\\&=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{40}}\right)\\a&\approx 0{,}156918\cdot R,\end{aligned}}}$

durch Umformen erhält man den Umkreisradius ${\displaystyle R}$

${\displaystyle {\begin{aligned}R&={\frac {a}{2\cdot \sin \left({\frac {180^{\circ }}{40}}\right)}}\\R&\approx {\frac {a}{0{,}156918}}\end{aligned}}}$

Der Inkreisradius ${\displaystyle r}$ ist die Höhe eines Teildreiecks, senkrecht zur Seitenlänge ${\displaystyle a}$ des Vierzigecks. Wird zur Berechnung wieder das gleiche rechtwinklige Dreieck wie bei der Seitenlänge verwendet, gilt für den Inkreisradius ${\displaystyle r}$

${\displaystyle {\begin{aligned}r&=R\cdot \cos \left({\frac {\mu }{2}}\right)=R\cdot \cos \left({\frac {180^{\circ }}{40}}\right)\\r&\approx 0{,}996917\cdot R\end{aligned}}}$

Die Höhe ${\displaystyle h}$ eines regelmäßigen Vierzigecks ergibt sich aus der Verdopplung des Inkreisradius ${\displaystyle r}$.

${\displaystyle h=2\cdot r}$

${\displaystyle h\approx 1{,}993834\cdot R}$

Die Fläche eines regelmäßigen n-Ecks berechnet sich aus dem Umkreisradius ${\displaystyle R}$ nach der Formel:

${\displaystyle A=n\cdot {\frac {\,R^{2}}{2}}\cdot \sin \left({\frac {360^{\circ }}{n}}\right)}$.

Für das Vierzigeck (n=40) also:

${\displaystyle A=20\cdot R^{2}\cdot \sin(9^{\circ })}$.

Der Winkel von 9° ist mit Zirkel und Lineal konstruierbar und sein Sinus hat den Wert:

${\displaystyle \sin(9^{\circ })={\frac {1}{8}}\cdot \left({\sqrt {2}}\cdot \left({\sqrt {5}}+1\right)-2\cdot {\sqrt {5-{\sqrt {5}}}}\right)}$

Eingesetzt ergibt sich:

${\displaystyle A=20\cdot R^{2}\cdot {\frac {1}{8}}\cdot \left({\sqrt {2}}\cdot \left({\sqrt {5}}+1\right)-2\cdot {\sqrt {5-{\sqrt {5}}}}\right)}$

${\displaystyle A=R^{2}\cdot {\frac {5}{2}}\left({\sqrt {2}}\cdot \left({\sqrt {5}}+1\right)-2\cdot {\sqrt {5-{\sqrt {5}}}}\right)}$

${\displaystyle A\approx 3{,}1286893\cdot R^{2}}$

Das Vierzigeck besitzt ${\displaystyle {\frac {40(40-3)}{2}}=740}$ Diagonalen. Die Diagonalen haben 19 verschiedene Längen.

Länge L der Seite und der Diagonale über N Seiten im Verhältnis zum Umkreisradius R
N L / R 11) 0,156918 2 0,312869 3 0,466891 4 0,618034	N L / R 5 0,765367 6 0,907981 7 1,044997 8 1,175571	N L / R 9 1,298896 10 1,414214 11 1,520812 12 1,618034	N L / R 13 1,705280 14 1,782013 15 1,847759 16 1,902113	N L / R 17 1,944740 18 1,975377 19 1,993835 20 2,000000

¹⁾ Seite des Vierzigecks.

Ein regelmäßiges Vierzigeck kann allein, wie in Regelmäßiges Vierzigeck begründet, mit Zirkel und Lineal konstruiert werden.

Die Konstruktion im Bild 1 ist ähnlich der des Fünfecks bei gegebenem Umkreis. Darin ist die Strecke ${\displaystyle {\overline {EF}}}$ die Seitenlänge und der Winkel ${\displaystyle GME=72^{\circ }}$ der Zentriwinkel des regelmäßigen Fünfecks.

Die gepunkteten Linien sind für die Konstruktion nicht erforderlich, sie dienen lediglich zur Veranschaulichung der folgenden Beschreibung.

Es beginnt mit dem gegebenen Durchmessers ${\displaystyle {\overline {AB}}}$ und dessen Halbierung im Mittelpunkt ${\displaystyle M.}$ Nach dem Ziehen des Umkreises um ${\displaystyle M}$ durch ${\displaystyle A}$ wird die zu ${\displaystyle {\overline {AB}}}$ orthogonale Mittelachse eingezeichnet; Schnittpunkte sind ${\displaystyle D}$ und der erste Eckpunkt ${\displaystyle E_{1}}$ des entstehenden Vierzigecks. Es folgt die Halbierung der Strecke ${\displaystyle {\overline {AM}}}$ in ${\displaystyle H}$, dabei ergeben sich die Schnittpunkte ${\displaystyle F}$ und ${\displaystyle G}$ auf dem Umkreis. Nun wird ein Kreisbogen um ${\displaystyle H}$ mit dem Radius ${\displaystyle |HE_{1}|}$ ab ${\displaystyle E_{1}}$ gezogen, bis er die Strecke ${\displaystyle {\overline {MB}}}$ in ${\displaystyle J}$ schneidet. Der Punkt ${\displaystyle J}$ teilt somit die Strecke ${\displaystyle {\overline {MB}}}$ im Verhältnis des goldenen Schnitts. Es ist das Ergebnis aus der Teilung der Strecke ${\displaystyle {\overline {AJ}}}$ in ${\displaystyle M}$ im goldenen Schnitt durch äußere Teilung. Nach dem Übertragen der Strecke ${\displaystyle {\overline {E_{1}J}}}$ – die Seitenlänge eines regelmäßigen Fünfecks – ab ${\displaystyle B}$ auf den Umkreis, ergibt sich der Eckpunkt ${\displaystyle E_{39}.}$ Halbiert man nun den Winkel ${\displaystyle E_{1}ME_{39}}$ ergibt sich der Eckpunkt ${\displaystyle E_{40}}$. Die Verbindung des Eckpunktes ${\displaystyle E_{1}}$ mit ${\displaystyle E_{40}}$ erzeugt die erste Seitenlänge ${\displaystyle a}$ des Vierzigecks. Jetzt noch die fehlenden Eckpunkte gegen den Uhrzeigersinn auf den Umkreis festlegen und abschließend die benachbarten Eckpunkte miteinander verbinden. Somit ist das regelmäßige Vierzigeck konstruiert.

F. A. Hegenberg stellt im Jahr 1822 in seinem Werk Vollständiges Lehrbuch der reinen Elementar–Mathematik, Zweiter Theil, im Kapitel Konstruktionen der Linien und ebenen Figuren, Aufgaben und deren Auflösungen u. a. auch zum Vierzigeck.

Unter § 776 stellt er die Aufgabe zu einem Polygon mit ${\displaystyle n}$ Seiten:

und zeigt dazu im darauffolgenden zweiten Absatz deren Auflösung:

Die Konstruktion im Bild 2 ähnelt der des Zwanzigecks bei gegebener Seitenlänge.

Zuerst werden die Enden der Seitenlänge ${\displaystyle a}$ mit den ersten Eckpunkten ${\displaystyle E_{1}}$ (rechts) und ${\displaystyle E_{40}}$ bezeichnet, anschließend wird die Seitenlänge ${\displaystyle a}$ über ${\displaystyle E_{1}}$ hinaus verlängert. Es folgt je ein Kreisbogen mit dem Radius ${\displaystyle a}$ um die Punkte ${\displaystyle E_{1}}$ und ${\displaystyle E_{40}}$; deren Schnittpunkte sind ${\displaystyle A}$ und ${\displaystyle B.}$ Anschließend wird eine Halbgerade ab ${\displaystyle B}$ durch ${\displaystyle A}$ gezogen; sie halbiert die Seitenlänge ${\displaystyle a}$ in ${\displaystyle C.}$ Eine Senkrechte auf ${\displaystyle {\overline {E_{1}E_{40}}}}$ ab ${\displaystyle E_{1}}$ schließt sich an und erzeugt den Schnittpunkt ${\displaystyle D.}$ Danach wird ein Kreisbogen um ${\displaystyle C}$ mit dem Radius ${\displaystyle |E_{40}D|}$ gezogen; dabei ergibt sich der Schnittpunkt ${\displaystyle F}$ auf der Verlängerung. Die Strecke ${\displaystyle {\overline {E_{40}F}}}$ ist somit nach dem goldenen Schnitt mit äußerer Teilung geteilt. Jetzt wird um ${\displaystyle E_{40}}$ ein Kreisbogen mit dem Radius ${\displaystyle {\overline {E_{40}F}}}$ geschlagen, der die Halbgerade in ${\displaystyle G}$ schneidet. In dem damit entstandenen gleichschenkligen Dreieck ${\displaystyle E_{40}E_{1}G}$ entspricht der Winkel am Winkelscheitel ${\displaystyle G}$ dem Zentriwinkel (hier mit ${\displaystyle \mu '}$ bezeichnet) eines regelmäßigen Zehnecks,

denn bei einer Seitenlänge ${\displaystyle a=1}$ gilt im rechtwinkligen Dreieck ${\displaystyle E_{40}CG}$

${\displaystyle {\begin{aligned}\sin \left({\frac {1}{2}}\mu '\right)&={\frac {\frac {a}{2}}{{\frac {1}{2}}+{\frac {\sqrt {5}}{2}}}}={\frac {a}{2\cdot \left({\frac {1}{2}}+{\frac {\sqrt {5}}{2}}\right)}}\end{aligned}}}$

mit eingesetzten Werten

${\displaystyle {\begin{aligned}\sin \left({\frac {\mu '}{2}}\right)&={\frac {0{,}5}{{\frac {1}{2}}+{\frac {\sqrt {5}}{2}}}}\\\end{aligned}}}$

daraus folgt für Winkel ${\displaystyle {\frac {\mu '}{2}}}$

${\displaystyle {\begin{aligned}{\frac {\mu '}{2}}&=\arcsin \left({\frac {0{,}5}{{\frac {1}{2}}+{\frac {\sqrt {5}}{2}}}}\right)=18^{\circ }\end{aligned}}}$

somit ist der Winkel ${\displaystyle \mu '=36^{\circ }}$ und damit gleich dem Zentriwinkel des Zehnecks.

Es geht weiter mit dem Kreisbogen um den Punkt ${\displaystyle G}$ mit dem Radius ${\displaystyle {\overline {E_{40}G}}}$; er schneidet in ${\displaystyle H}$ die Halbgerade, die ab ${\displaystyle B}$ durch ${\displaystyle A}$ verläuft. Wegen ${\displaystyle {\overline {E_{40}G}}={\overline {GH}}}$ ist nach dem Zentriwinkelsatz die Winkelweite am Winkelscheitel ${\displaystyle H}$ des gleichschenkligen Dreiecks ${\displaystyle E_{40}E_{1}H}$ halb so groß ${\displaystyle \left(18^{\circ }\right),}$ als die Winkelweite ${\displaystyle \mu '=36^{\circ }}$ am Winkelscheitel ${\displaystyle G}$ des gleichschenkligen Dreiecks ${\displaystyle E_{40}E_{1}G.}$ Ein weiterer Kreisbogen, dieses Mal um den Punkt ${\displaystyle H}$ mit dem Radius ${\displaystyle {\overline {E_{40}H}}}$, der dieselbe Halbgerade in ${\displaystyle M}$ schneidet, erzeugt demzufolge am Winkelscheitel ${\displaystyle M}$ den Zentriwinkel ${\displaystyle \mu =9^{\circ }}$ des Vierzigecks.

Jetzt noch den Umkreis um den Mittelpunkt ${\displaystyle M}$ ziehen, die noch fehlenden Eckpunkte gegen den Uhrzeigersinn auf den Umkreis festlegen und abschließend die benachbarten Eckpunkte miteinander verbinden. Somit ist das regelmäßige Vierzigeck konstruiert.

Es ergibt sich, wenn beim Verbinden der vierzig Eckpunkte jedes Mal mindestens einer übersprungen wird und die somit erzeugten Sehnen gleich lang sind. Notiert werden solche regelmäßigen Sterne mit Schläfli-Symbolen ${\displaystyle \left\{n/k\right\}}$, wobei ${\displaystyle n}$ die Anzahl der Eckpunkte angibt und jeder ${\displaystyle k}$-te Punkt verbunden wird.

Es gibt nur sieben regelmäßige Vierzigstrahlsterne.

Die „Sterne“ mit den Symbolen {40/2} und {40/38} sind regelmäßige Zwanzigecke, {40/4} und {40/36} regelmäßige Zehnecke, {40/5} und {40/35} regelmäßige Achtecke, {40/8} und {40/32} regelmäßige Fünfecke, {40/10} und {40/30} regelmäßige Vierecke. Die Sterne mit den Symbolen {40/6} und {40/34}, {40/14} und {40/26} sowie {40/18} und {40/22} sind regelmäßige Zwanzigstrahlsterne, {40/12} und {40/28} sind regelmäßige Zehnstrahlsterne, {40/15} und {40/25} regelmäßige Achtstrahlsterne und schließlich {40/16} und {40/24} regelmäßige Pentagramme.

• Regelmäßige Vierzigstrahlsterne
• 
  ${\displaystyle \left\{40/3\right\}{,}\ \left\{40/37\right\}}$
• 
  ${\displaystyle \left\{40/7\right\}{,}\ \left\{40/33\right\}}$
• 
  ${\displaystyle \left\{40/9\right\}{,}\ \left\{40/31\right\}}$
• 
  ${\displaystyle \left\{40/11\right\}{,}\ \left\{40/29\right\}}$
• 
  ${\displaystyle \left\{40/13\right\}{,}\ \left\{40/27\right\}}$
• 
  ${\displaystyle \left\{40/17\right\}{,}\ \left\{40/23\right\}}$
• 
  ${\displaystyle \left\{40/19\right\}{,}\ \left\{40/21\right\}}$

• Vierzigeckiges Walter Payton's Roundhouse (Former)

1. ↑ F. A. Hegenberg: Vollständiges Lehrbuch der reinen Elementar–Mathematik, Zweiter Theil. Theodor Christian Friedrich Enslin, 1822, Online-Kopie (Google) S. 381, § 776, Deckblatt; abgerufen am 20. April 2018